鶴亀算を方程式で解くのはNG?
ジュース47ダースは何本か 47×12は不正解の怪:朝日新聞デジタル
中学入試の算数で、本来中学校以降でしか習わない方程式を使うとダメなのかって話です。
うちの子はいまだ塾には通わせず、受験向け(受験させるつもりはないけど)の算数は私が教えています。で、小学生の解き方(算数)と中学生以降の解き方(数学)の両方で解ける場合は、その両方を指導しています。
うちは受験させるつもりがなくて、学力の向上と数学の面白さを教えるのが目的なのでこういうことをしているのですが、中学受験させるつもりであれば数学的手法を教える必要はありません。この記事にあるように、完全なマルをもらえなくなる可能性があるからです。
では数学のセンスの育成という点ではどちらの教え方の方が良いのでしょうか。私が思うに、やはり「両方教えるべき」です。数学的手法の方が後から学ぶので高度なのだから、そちらだけ知っていれば良いじゃんと思われるかもしれませんが、違うんですよ。
算数を数学で解くのは、「単なる計算問題」にしてしまうのです。本来算数はイメージで捉えて解くものなんですよ。
具体例を挙げましょう。
このサイトから問題を拝借します。
「鶴と亀が合わせて20匹、足は64本、それぞれの頭数は?」
鶴亀算:算数の解き方
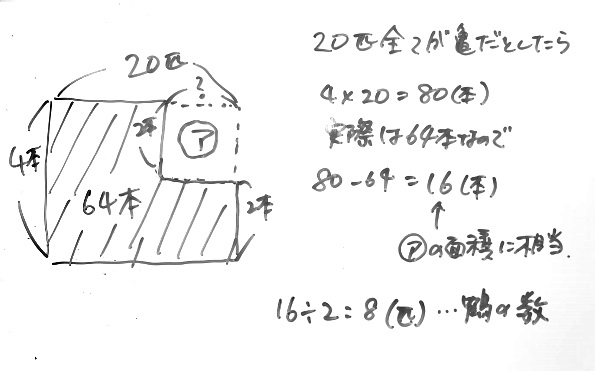
縦を1匹あたりの足の本数、横を鶴と亀の数の合計にした2つの長方形で表します。こうすると、その面積が合計の足の数ということになります。
20匹全てが亀だとしたら、
4×20=80(本)……大きな長方形の面積が合計の足の数
ということになりますが、実際は64本で16本のギャップがあります。そのギャップが(ア)の面積に相当します。
長方形(ア)の一つの辺の長さは4-2で2と分かりますから、16÷2でもう一辺が算出されます。これが鶴の頭数=8となります。
こうやって概念図で表して、イメージとして捉えるのが算数の手法です。
鶴亀算:数学の解き方
一方、数学では。
「亀の頭数をxとする」とさえすれば、
4x+2(20-x)=64
という1つの方程式で済みます。あとはこれを整理すると
4x-2x=64-40
x=12
と導かれます。
何とも淡白ですね。そして、実に簡単です。
中学受験を経験した方なら、中学で数学を学んだ時に思ったはずです。
「こんな簡単な方法があるなら最初から教えてくれよ!」
と。
ところが、それは算数の手法をやった後だからそう思うのであって、数学だけだと何をやってるかを直感的に理解できないんですよね。なぜなら、これは単なる計算方法でしかないからです。
もっとも、鶴亀算の例では、数学と言ってもここでやってることは代数なので「計算方法」でしかないわけですが、数学=計算方法ではありません。
算数と数学とでは脳の使い方が違う
同一の問題から正解を導く方法が2つあったとしても、おそらく脳の使い方はかなり違うはずです。ザックリしたイメージですが、概念図をすっ飛ばして解けてしまう数学が左脳しか使わないのに対し、算数では右脳もグルグル回っている感じですね。
しかしこの鶴亀算、公立小学校では習わないまま卒業しちゃいますよね。で、中学に入ったら数学になってしまう。むむ…なんかもったいない話です。すごく面白い問題なのに。
ってことで、次は「掛け算の順序」問題へ。









































コメント