↑からの続き。
さてさて、この記事で扱われているもう一つの問題、「掛け算の順序」についてお話します。いつかはこれを…と思っていた話題ですが、ついに解禁。
なぜ小学校では掛け算の順序を決めてしまうのでしょうか。
簡単に言えば、物事を説明されてそれを数式に直す際、ちゃんと整理して考えられているかどうかを肯定派は見ているわけです。その結果、
「1セット当たりの数」を基本にして、それが何セットあるかを計算する。
というやり方を学校は教えるわけですよ。しかし、このやり方には極めて大きな欠陥があります。
「1セット当たりの数」と言うのは、言わば会計表記的なんですね。買い物した時のレシートとか見積書だとかの類です。しかし、数学とは会計なのでしょうか?というともちろん否です。会計は数学(算術)ですが、数学=会計ではありません。
欠陥その1「だったら割り算にも順序があるの?」
「5人の子どもに3個ずつ飴をあげます。合計何個?」
という問題であれば、
3×5=15
で正解になります。
5×3=15
は△にするのが今の学校のやり方。なぜなら掛け算には順序があるのですから。
ではこれを割り算の問題にしましょう。
「15個の飴を5人に均等に分けます。1人当たり何個?」
15÷5=3
ですね。「15」と「3」の単位も揃っています。
「15個の飴を3個ずつ分けたら何人にあげられる?」
これももちろん、
15÷3=5
…………あれ?「15」と「5」は単位が違いますね?
それに前の問題と数字を書く順序が変わっています。
そうなんです。「掛け算に順序がある」なんてことを言ってしまうと、割り算が説明できなくなるんですよ。
![]()
欠陥その2「長方形の面積は?」
「2辺が5cmと3cmの長方形があります。面積は?」
という問題があったとして、式はどうしましょうか。
5×3でも3×5でも良いなんてことはありませんよね。なんせ、掛け算には順序が決められてるんだから!
いやしかし、言うまでもなく、長方形の面積の求め方に順序なんてものはありません。
そもそもどちらを先に持ってこようが、算出されるのは面積(cm2)であって、単位を揃えることができないのですよ。
それとも、どっちかを「縦」に決めないと数式も書けないとか?
欠陥その3「電力は?」
電気の基本的な式に、
電流(アンペア)×電圧(ボルト)=電力(ワット)
というのがあります。
これまた単位がバラバラで、順序もへったくれもありません。掛け算に順序があるとしたら、これも説明できなくなります。
ではどう考えればいいのか
そもそも掛け算とは何でしょうか。これは子供には難しい説明になりますが、掛け算の本質は「次元を1個上げる」ということになるんです。ピンと来ない?
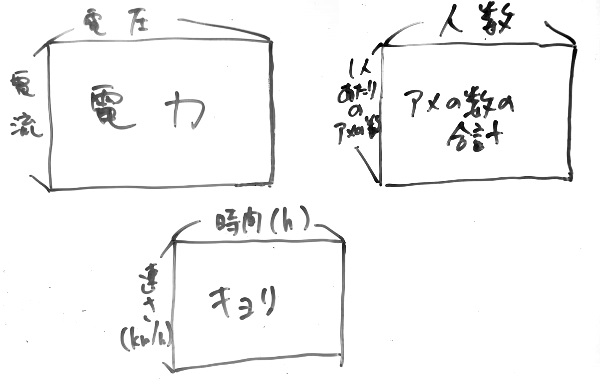
例えば長方形の面積だと、「長さ」に「長さ」を掛けて「面積」を出します。「長さ」は1次元で、その1次元同士を掛けることによって面積という2次元の数値が導かれるわけです。
この場合の「長さ」を因数と言いますが、因数の数=次元になるんですよ。もうちょい簡単に言うと、2つの数を掛ける掛け算の場合、その答えは平面として扱うことができるわけです。もちろん、そこにさらに「長さ」を掛けると、「体積」というさらに1次元上がった数値が出てきます。
例えばですね、「1時間あたりに50km進む車が3時間走ったらその距離は?」という場合、
50(km)×3=150(km)
とすると、一見単位が揃っていてスッキリした気がします。ところが、50と150は全く性質の違う数なんですよ。
正確に書くと、
50km/h×3h=150km
なんです。
だって、
距離×時間=距離
ではなく、
速さ×時間=距離
って習いましたよね?「速さ」と「距離」は違うものですよね?
「km/h」と「km」は実は違う単位なのに、いかにも同じ単位であるかのように教えてしまうから掛け算の本質を見落としてしまうことになるわけです。
飴であれば、
3個/人×5人=15個
となるわけです。
「/人」の「/」は「パー」つまり、「1ホニャララあたり」という、まさに1セットを表します。「1kgあたり」とか「1時間あたり」とかですね。この場合はだと「人」が分母に来る分数で表されており、「“人”の逆数」です。「“人”の逆数」ということは、「人」を掛けることによって消失します。だから最終的に残る単位は「個」だけになるんです。
この単位さえしっかり認識しておけば、掛け算の順序なんてどうでも良くなるんです。
学校の教え方も分からんわけではないが
たしかに、単位を揃える(揃ってないんだけど)ということは、物事をきれいに整理して考えるという点では悪いことではないのかもしれません。しかし、くどく言うように、「掛け算の本質を見落とす」という副作用はいささか強いような気がするんです。
むしろ、
「3人ずつ5列に並ぶ」のと「5人ずつ3列に並ぶ」のは、「合計人数を出す」という点においては同じ=掛け算の順序はどうでも良い、と教える方が後の数学の理解に繋がるのではないかと思います。
掛けられる数に掛ける数があるんじゃなくて、そこにあるのは因数(掛け算の要素となる数)と積(掛け算の答え)だけなのですよ。
どんな性質の数字であれ、2つの数を掛け合わせるということは平面的数量として扱うことができる=四角形(平面)として描き表すことができるということになるのです。
とこんな感じでどうですか?







































コメント
◯「なぜ小学校では掛け算の順序を決めてしまうのでしょうか。……物事を説明されてそれを数式に直す際、ちゃんと整理して考えられているかどうかを肯定派は見ている」
―― これは正しいと思います。
△「数学とは会計なのでしょうか?というともちろん否です。会計は数学(算術)ですが、数学=会計ではありません。」
―― 会計が数学の一部なら、「会計表記的」なものも数学的なものですよね。ですから、「1セット当たりの数」も数学的なものです。もちろん、それは数学の、初等段階で学ぶ、数学のほんの一部にすぎませんが、でも、その理屈に従えば、数学的なものです(会計学者は反対するかもしれませんが)。
×「「だったら割り算にも順序があるの?」」「「掛け算に順序がある」なんてことを言ってしまうと、割り算が説明できなくなるんですよ。」
―― わり算が、割られる数と割る数を取り違えたら、計算結果(商)が違ってきてしまいますので、順序は当然あります。あなたは違うのかもしれませんが、順序派も自由派も普通は、わり算に順序があるとする点で一致しています。
算数の教科書は、かけ算の順序を利用して、うまくわり算を説明しています。
小学校では、かけ算は、1つ分×いくつ分=全部の数、の図式で習います。わり算には、等分除と包含除がありますが、かけ算との関係で言えば、等分除は、全部の数といくつ分がわかっているときに、1つ分を求めるわり算です。これに対して、包含除は全部の数と1つ分がわかっているときに、いくつ分を求めるわり算です。
等分除「15個の飴を5人に均等に分けます。1人当たり何個?」
15個÷5=3個 〈⬜×5=15全部の数〉の⬜を求めるわり算
包含除「15個の飴を3個ずつ分けたら何人にあげられる?」
15個÷3個=5 〈3×⬜=15〉の⬜を求めるわり算
順序派が、かけ算について、3個×5=15個のように、被乗数と答え(積)で単位・助数詞が一致すると言うことはありますが、わり算の割られる数と答え(商)の単位・助数詞が一致するなどとは主張しません。
もちろん、すでに書いたように、わり算では、割られる数と割る数のあいだには順序はあります。
×「欠陥その3「電力は?」欠陥その2「長方形の面積は?」
―― 電力=電流×電圧も、長方形の面積=縦×横の公式に使われているかけ算は、因数×因数のかけ算で、小学校で習う1つ分×いくつ分、基準量×倍(割合)のような非対称なかけ算ではありません。因数×因数の対称的なかけ算は中学以降に、数学や理科で学ぶかけ算です。
電力は小学生ではまだ学習しませんから、論外です。長方形の面積は4年次に学びますが、一辺が1cmの単位正方形(1cm^2)を考えて、その単位正方形がいくつあるのかで、長方形の広さを表そうとしています。つまり、〈1つ分(単位正方形)×いくつ分〉のかけ算を使っています。小学校では、また、長さと長さを掛け合わせて面積と言う新しい次元を作り出す、というところまで行かないのです。
速さも、1つ分×いくつ分の適用で考えられる範囲での限定的な速度概念です。小学校では、一時間に3kmで5時間走るのは、5枚の皿に3つずつリンゴを載せるのと、同じ構造で考えられています。小学校では、まず、ここから速度の学習を始めるのです。方向を含めた高度な速度概念は、難しすぎるので、教えていません。
×「掛けられる数に掛ける数があるんじゃなくて、そこにあるのは因数(掛け算の要素となる数)と積(掛け算の答え)だけなのですよ。」
―― かけ算には、因数×因数の掛け算だけでなく、1つ分(被乗数)×いくつ分(乗数)のかけ算もあります。どちらも、りっぱなかけ算だと思います。因数×因数だけがかけ算の本質ではありません。ただ、因数×因数のかけ算は、小学生には抽象的すぎるので、小学校では、かけ算の意味を1つ分×いくつ分に限定して教えているのです。基準量×割合、単価×数量、速さ×時間などは、そのバリエーションです。
△「「3人ずつ5列に並ぶ」のと「5人ずつ3列に並ぶ」のは、「合計人数を出す」という点においては同じ=掛け算の順序はどうでも良い、と教える方が後の数学の理解に繋がるのではないかと思います。」
―― 算数では、3つずつのグループを作るか、5つずつのグループを作るかの区別は、依然として重要です。小学生はその思考の発達段階からして事物に従ってものを考えるので、3×5と5×3では、計算結果が同じでも、事物の配列が異なり、したがって、意味は違うと理解されます。「3連プリンを5パック、全部で何個?」という文章題では、3×5が正しい式です。
でも、中学に入ると、文字式が導入されます。ただabと書いてあっても、どちらが1つ分かはわかりません。中3になると、因数分解を学びます。12は4と3に因数分解されますが、どちらが1つ分かはわかりません。4と3が対等な因数として掛け合わされて、12という積を構成しています。
×「「人の逆数」ということは、「人」を掛けることによって消失します。だから最終的に残る単位は「個」だけになるんです。
この単位さえしっかり認識しておけば、掛け算の順序なんてどうでも良くなるんです。」
―― 数教協の組み立て単位ですね。約分をまだやってないうちから、数字ではない単位の約分なんで、難しすぎないでしょうか。日本の算数教育でも、1970年代までは、組み立て単位ではありませんが、式に単位・助数詞を付けていました。でも、かけ算の順序はありました。単位を付ければかけ算の順序はなくなるというのは、理論的なものです。実際には、単位を付けた上で、かつ、単位あたり量を先にして順序を固定することになると思います。
>一辺が1cmの単位正方形(1cm^2)を考えて、その単位正方形がいくつあるのかで、長方形の広さを表そうとしています。つまり、〈1つ分(単位正方形)×いくつ分〉のかけ算を使っています。
なら、5人に飴を3個ずつ配る場合も1個×3×5または1個×5×3で良いのではないでしょうか。
○○○○○葡萄味
○○○○○林檎味
○○○○○蜜柑味
太次詫花麗
郎郎助子子
>小学校では、かけ算の意味を1つ分×いくつ分に限定して教えているのです。基準量×割合、単価×数量、速さ×時間などは、そのバリエーションです。
基準量×割合は往々にして割合の方が(小数表記の場合)1つ分ですよね。
図形の回転に対して面積が保たれるのは自明ではない(素人が変な記事を書かないように)