モンティ・ホール問題とは
私の大好きな数学の問題で「モンティ・ホール問題」というのがあります。
ご存知の方も多いでしょう。
これを小学校高学年の息子に教えてみたんですわ。
大人でもよく分からないこの問題を子供に教えてどうするのか?
いやいや、この問題の「不思議さ」が理解できればとりあえずそれで良いんです。
とにもかくにもまずはモンティ・ホール問題そのものがどんなものかを説明します。
これはひとつのゲームでして、3つの扉から景品の隠れた扉を当てるというもの。かつてアメリカで放送されていたテレビ番組『Let’s Make a Deal』の中で行われていたゲームで、その番組の司会者の名がモンティ・ホールでした。
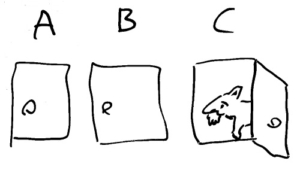
1.3つの扉がある。
2.扉のうち1つには新車、残りの2つにはヤギが入っている。ヤギはつまりハズレ。
3.プレイヤーに1つの扉を選ばせる。
4.モンティはプレイヤーが選択しなかった残りの2つのうち、ヤギが入っている扉を開ける。
5.モンティが改めてプレイヤーに「今なら選択肢を変えても良いがどうする?」と聞く。
さて、プレイヤーから見て、
- 選択を変えない方が得
- 選択を変えた方が得
- どちらも確率は同じ
のどれになるか、というのがこの問題です。
さて、あなたはどれだと思いますか?この問題をここで初めて知った人は、多くが「どちらも確率は同じ」を選ぶと思います。
マリリン・ボス・サバントの示した正解
これが話題になったのは、IQ200オーバーの天才にして女性コラムニストであるマリリン・ボス・サバントが、モンティ・ホール問題についての読者の質問に答えたことが発端でした。
彼女は
「選択を変えると当たる確率は2倍になって得」
という、多くの人の直観に反する驚きの回答をして、プロの数学者まで巻き込む学術論争に発展したんだとか。
後に解説する通り、彼女の答えは正解なのですが、面白いのはこれが1990年と言うかなり最近の話であることと、くだんの番組がどうやら60年代から放送されていたことです。なぜそれまで誰も疑問に思わなかったのでしょうか?
さらに古くは「3囚人のパラドックス」という数学の問題があり、彼女はそれを知っていたものと思われますが、彼女の回答に納得しなかった数学者は知らなかったのでしょうか?
モンティ・ホール問題の解説
では解説です。
もし選択を変えなければ、当たる確率は1/3。
これに解説は要らないと思います。
問題は、選択を変えた場合にその確率が変わるのかという点。
<最初の選択がAだった場合>Aが当たりの場合、もう一方(BまたはCの扉が開かれていない方)に移動→ハズレ
Bが当たりの場合、Bに移動(Cという選択肢が消えているため)→当たり
Cが当たりの場合、Cに移動(Bという選択肢が消えているため)→当たり
どうでしょうか。3パターンのうち、2つが当たりになるのですから、確率は2/3になります。
同様に、
<最初の選択がBだった場合>Aが当たりの場合→当たり
Bが当たりの場合→はずれ
Cが当たりの場合→当たり
やはり同じです。
もちろんCでも同様。
さて、どういうことなのでしょうか?
こうやって表にすれば証明は簡単なのですが、何しろ直感がジャマをしてなかなか理解に至りません。
モンティ・ホール問題、私なりの説明
で、ここからが私なりの説明になります。後ほど書く、子供にどう教えれば直感的な理解が得られるか、を考えてこの説明に至りました。
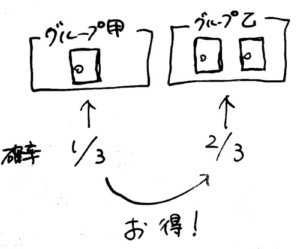
自分が選んだカード1枚を「グループ甲」、残りの2枚を「グループ乙」に分けます。
グループ甲が当たりの確率は当然1/3。
では、グループ乙のが当たりの確率は?
(1/3)+(1/3)=2/3
になります。あるいは、
1-(1/3)=2/3
という式でも構いません。
※断っておきますが、カッコは分かりやすいように付けているだけです。
もし、ここでモンティが、ただ「今なら選択をし直せますよ」とだけ言ったのであれば、選択を変えずにいようが変えようが確率は1/3のままです。
数式にすると、
(2/3)×(1/2)=1/3
ところがモンティは、間違いなくハズレである1枚を取り除いてくれるんですね。プレイヤーが勘とか運とか超能力を使わずとも、です。
つまり、「選択肢を変える」ということは、確率2/3のグループ乙に移動するけどその後BかCを選ぶ必要はない、ってことなんです。
数式にすると、「×(1/2)」が削除されて、2/3がそのまま残るということ。
表現を変えてみるとですね、モンティがハズレを1つ削除せず、
「Aのままで良いですか?今、選択を変えるならBとCどちらに入ってても当たりってことにしますよ」
と言ってるのと同じなんです。
麻雀で言えば、2+4のカンチャン待ちで5が来て、4+5の両面待ちになり、かつ役が変わらないという状況です。特殊なケースでなければ、2を捨てて両面待ちにするのが当たり前ですね。え、麻雀知らない?
ではまた別の表現を使いましょう。
要するにこのゲーム、A,B,Cという3つの選択肢があるように見えるんですが、実際にプレイヤーが選ぶのは「AかA以外か」(「BかB以外か」「CかC以外か」)という2つの選択肢から選んでいるだけなのです。
![]()
モンティ・ホール問題を子供にどう教えるか
さてさて、ここまでが長ーい前置きでここからが本題。
このモンティ・ホール問題を子供にどう教えるか、です。
対象年齢は小学5年生~中学3年生といったあたりでしょうか。
なんせ、特殊な数式も、ナンチャラの定理なんかも必要のない問題ですから、幅広い年齢で教えることができます。もちろん高校生だってかまいませんが、高校生ともなると親子でそんなにコミュニケーションもないでしょうからね。
この問題に限らず、うちでの教え方は、
「分かりやすい教材があるなら最初は手助けなしに勉強させ、逆にレクチャーさせる」
という方法をよく採ります。
モンティ・ホール問題は特に理系に限らず人気のある数学問題で、これについて解説されているウェブサイトはいくらでもあります。Youtubeにもあります。
それらを何パターンか見せた後に「さあ、お母(父)さんに教えてちょうだい」とやるわけです。
これを読んでいるあなたがが「お母さん」でこの手の話が苦手なら、お父さんのサポートを請いましょう。


















コメント